前情

手上是一批样本量（N=210）的纵向数据T1-T4, 数据有四个变量X2，X3，X4，X5与一个作为轨迹的变量X1
运用潜在增长模型的方法，计算X1变量T1-T3的截距和斜率作为自变量，控制四个变量的基线（协变量），并构建模型（参考：肖家乐, 申子姣, 李晓燕, 林丹华. (2023). 同伴侵害变化轨迹及其与抑郁情绪和外化问题的关系：共同增强还是风险易感. 心理学报, 55(6), 978-993.）

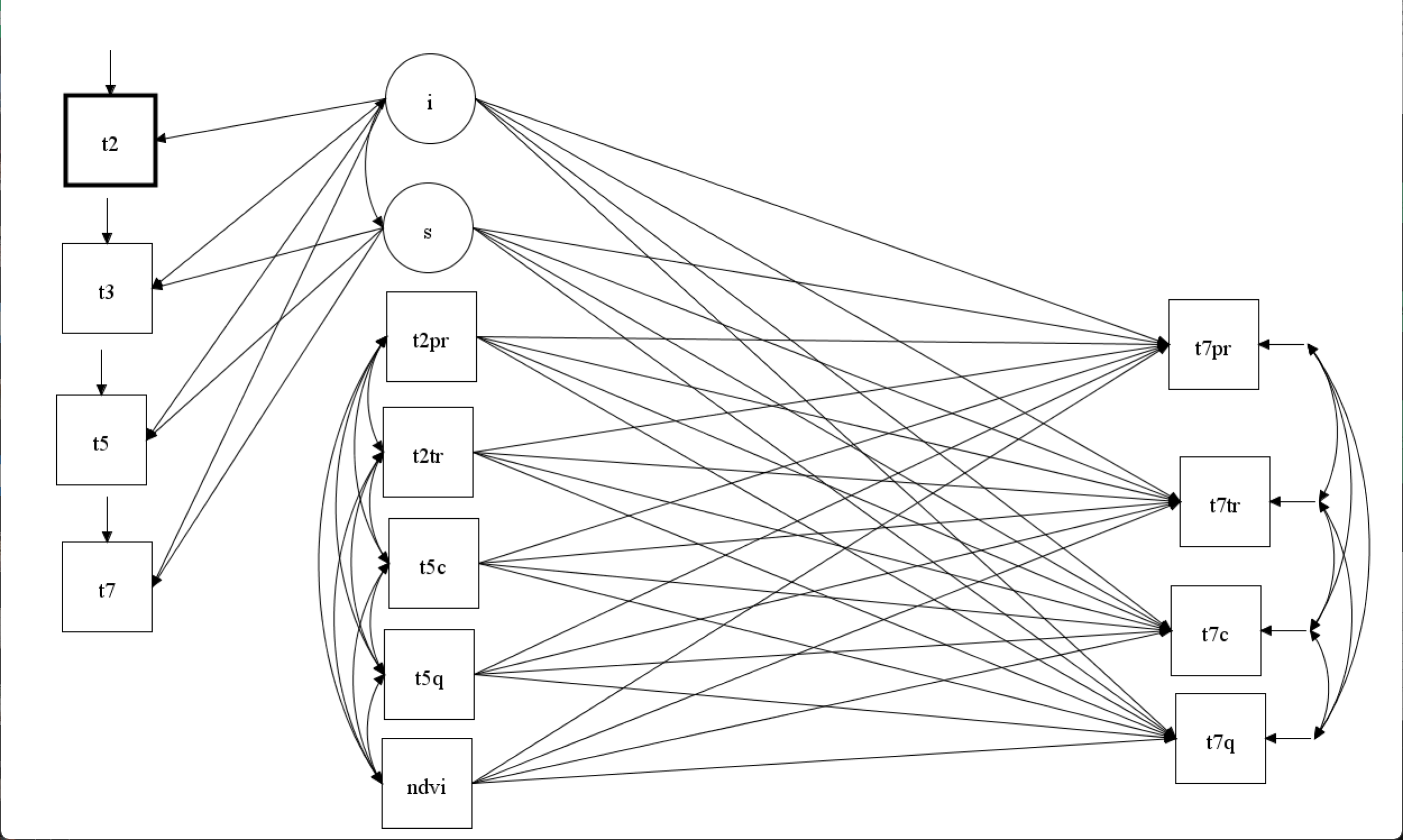
结果

`构建模型后发现问题残差方差为负数`
    `残差指的是真实值和预测值之间的差的绝对值，残差方差不可能为负数`
        `这被称为Heywood case`

总结

`小样本而模型复杂，并且预测变量之间存在高度相关会出现残差方差为负的情况，而无法拟合`

解决

施加参数约束 (Constraining Parameters)。这是最常用的技术手段。既然模型估计出了一个不合理的负值，我们就强行命令模型不许这样做。

优点：为什么这样做可能让模型拟合？等于帮计算机“做了一个决定”。模型之前为了拟合数据，把`T7TR`的残差方差“推”到了负数区域。现在您堵死了这条路，强迫它在“方差必须大于等于0”这个前提下去寻找一个最优解。这样模型就不会再因为算出负值而崩溃，从而有可能收敛并报告出拟合指数。

 槽点⚠️ 巨大的风险和代价： 将残差方差固定为0是一个非常强的假设。这等于在告诉世界：“我模型里的预测变量（i, s和所有协变量）已经100%完美地解释了T7TR和T7Q的所有变异，没有任何未解释的随机因素了。” 这在现实研究中几乎是不可能的。这样做虽然能得到结果，但可能会导致模型中其他参数的估计值出现偏差，并且您必须在论文中明确报告您施加了这个不合理的强约束。